DSP Enable lowers Sound Quality

[brian (Brian Luczkiewicz)]

Lowering the volume in the digital domain will reduce sound quality, that’s known. Here is how, on a simple level, I think Roon adjust the volume ( @brian can maybe confirm or explain it in more detail if needed):

Original input (16 bit for CD quality), is converted to a 64 bit double
Volume adjustment is made on the double value.
The double is converted back to 16 bit

The lowering of sound quality is partly because the resolution will be lowered (it might “remove” bits), but also because the conversion back to 16 bit will require rounding, and the rounding part is lost.

That’s true if you start with 16bit and end with 16bit, but that’s not what Roon does.

In Roon, if you start with 16bit and do a -3dB headroom adjustment, the process looks like this:

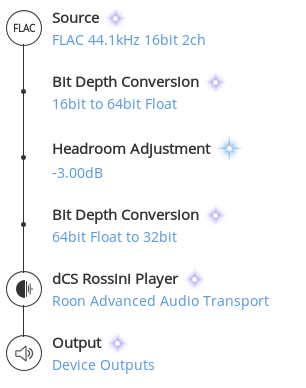
Notice that the stream going to the DAC is 32bits, not 16.

This is because Roon expands headroom when performing DSP to 64bits (since 64bit float is our intermediate format). Then, when it’s preparing to stream to the device, it converts to the widest format that the device supports. In this case, 32bit.

6dB = 1 bit. So a 3dB adjustment moves the audio down 1/2 of a bit. At the same time, we’ve expanded headroom to 32bits. You can mathematically reverse the adjustment without reducing the number of significant figures–so there is no information loss either. To be clear, this means you could:

• Start with a 16bit signed integer signal
• Convert to 64bit float
• Apply a -3dB gain adjustment
• Convert to 32bit signed integer
• Convert back to 64bit float
• Apply a +3dB gain adjustment
• Convert back to 16bit signed integer

And the output signal would be bit-perfect to the original. So from an information-theoretic perspective, the gain-adjusted 32bit signal is lossless.

That said, there are some ways that lowering the volume earlier in the playback chain can result in a reduced perception of quality despite the fact that no information about the signal is lost. For example:

• Psychoacoustics. Any test of a volume control that does not employ precise level-matching is flawed. Quieter statistically sounds worse
• After level matching, you may discover that the amplifier (or another component) does not perform equally well in all volume ranges.

The second one is particularly applicable to volume leveling–since the adjustments are often ~10-15dB. I like volume leveling, but not all amplifiers sound as good cranked 10dB louder to compensate, especially headphone amps.