… so what are your thoughts on this… any audible improvement by higher bit rate when the kHz is equal = 44.1?
In theory, more dynamics, more nuances in the volumes.
In practice, it depends on so many factors that you really need excellent material and excellent recording to see the difference.
In theory, just more headroom for editing/lower noise floor.
I can’t think of any recording for playback that needs more than 96 dB dynamic range.
Or calculations on the signal in general. Older devices, at least I hope that by now all newer devices are doing the conversion to their highest supported bit depth or higher before doing calculations, may quickly start loosing on resolution when a digital volume control gets used (the very reason for the bad reputation of digital volume controls) on a 16-bit signal in 16-bits only.
So in general, might aswell stick to 44.1 kHz 16 Bit… comes way cheaper and no real audible difference to 24 bit playback?
I have a few 44.1/24 bit albums, and I’m convinced they sound better than the 16 bit cuts. Whether this is down to re-mastering or expectation bias, I don’t know. The Beatles in 24 bit is a good example.
This was discussed at some length in this thread.
The bottom line is more bits = lower noise floor. That’s all it means.
For mastering a recording, you may need more that 16 bits. But, as a distribution medium, 16 bits gives you a noise floor low enough that there’s no point to going any further.
Or you could just skip the whole long-winded discussion and watch this video.
… so basically we are all being told and sold a lot of bollocks by the industry… 
I agree. But why wouldn’t one want to maintain the lower noise floor / greater dynamic range through the distribution media? Especially as the playback equipment becomes better?
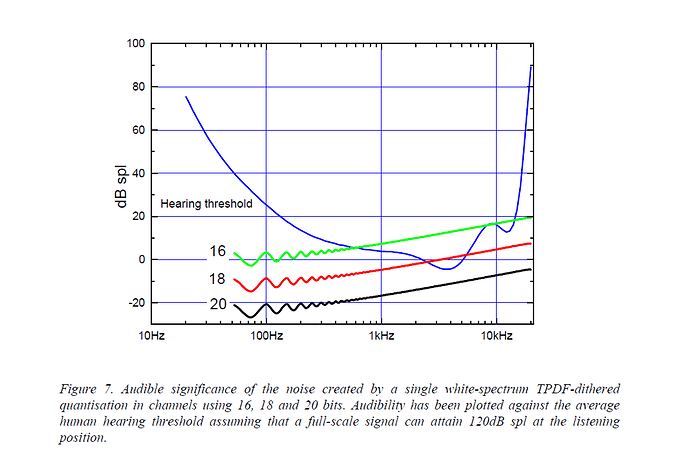
This graph from a paper that Bob Stuart wrote seems to address the issue quite succinctly. There is a range of hearing where we have sensitivity sufficient to perceive the higher noise floor inherent in a 16 bit PCM encoding.
I agree that the noise from all the other sources in the recording has to be low enough that these other noise sources don’t dominate. But I do think that the case for a word size > 16 bits is valid.
If you turn up the volume loud enough, you will always be able to hear the noise.
How loud do you need to crank up the volume here?
To obtain this graph, Stuart set 0dBFS = 120dB SPL at the listening position. Let’s recall what that means:
- Risk of instantaneous noise-induced hearing loss.
Is anyone going to risk permanent hearing loss, just so that they can experience the quantization noise at 16 bits just barely rising above the threshold of hearing?
Seriously?
And that is the best-case (or worst-case) scenario for being able to hear the quantization noise.
In any non-insane scenario, it is utterly inaudible.
(Also note that Stuart deliberately did not use noise-shaping dither – which moves the noise to higher frequencies, where the human ear is less sensitive. In the region plotted, noise-shaping would gain you another 4-6dB, which would make Stuart’s scenario even more far-fetched.)
Fair point.
I know that when I calibrate my system, the software wants me to put the level in the 70-75 dBSPL range at the listening position and that’s about as loud as I ever set the volume. Now that’s for pink noise so maybe the peak levels would be in the 90-100 dBSPL range? The graph shows that the 16 bit noise level is 15 or so dB above the hearing threshold. That would imply that the 16 bit noise would be audible at peak levels in the 100-105 dBSPL range? So there is still probably 10 dB or so of headroom. I agree it is likely inaudible but not insanely so.
Thanks for the discussion.
Welcome to the hi-fi world. Digital audio must be terrifying to the industry; imagine a medium that doesn’t wear out. Even CDs had a limited shelf life. How are you going to get people to buy the music all over again? A new format of some sort is the only hope!
As has been stated over and over and over again in this discussion increasing the bit depth DOES NOT increasing the dynamic range of the recording. Need proof? Just take any 24bit recording and check the dynamic range of the recording. Now decrease the bit depth to 16bits and recheck the dynamic range of the recording. It will be exactly the same. Each and every time.
The two of you are using the phrase “dynamic range” in slightly different (but equally valid) senses.
You’re talking about the dynamic range of the signal (the ratio of the loudest to the softest passages).
He’s talking about the dynamic range of the medium (the ratio of the loudest thing you could record to the inherent noise of the medium).
Obviously, you want the dynamic range of the medium to be greater than the dynamic range of the signal you are trying to record on it.
With 16 bit PCM, you get a dynamic range of the medium of 96 dB. If you use noise-shaping dither, you can push that to a little over 100 dB. That’s more than enough for any signal any sane person might want to listen to.
And more than enough for any musical performance that doesn’t include atomic explosions. Even 110 piece orchestras or heavy metal bands.
… so there is really no Argument to buy 24bit recordings at all and all the stuff Qobuz is selling is basically a rip off… I mean they sell 44.1 kHz 24bit recordings at rediculous prices vs regular CDs…
If you look at your music in your library you can see the dynamic range of all tracks. In my library I have a handful with 27 dB Range. And then it goes down quickly to 10 dB and less.
In the other thread mentioned by @Jacques_Distler is a comment from @Peter_Comeau who seems to work in the music industry:
So for me, when I stream I listen to the 24bit one, but to buy I just take the 16bit one.
I’m glad to read that my point is starting to get across. One rule to follow: marketing people know no limits and have no morals when it comes to trying to separate the consumer from their hard earned money.
I believe the standard calibration for pink noise test tones is -20 dBFS. So if we set -20 dBFS = 75 dB SPL then, yeah, 0 dBFS = 95 dB SPL.
According to Wikipedia
While 16-bit audio is typically thought to have 96 dB of dynamic range (see quantization distortion calculations), it can actually be increased to 120 dB using noise-shaped dither.[3]
With 4 (as opposed to 16) bits, triangular dither (as in Stuart’s example) gets you a noise floor that looks like this (750 Hz test tone):
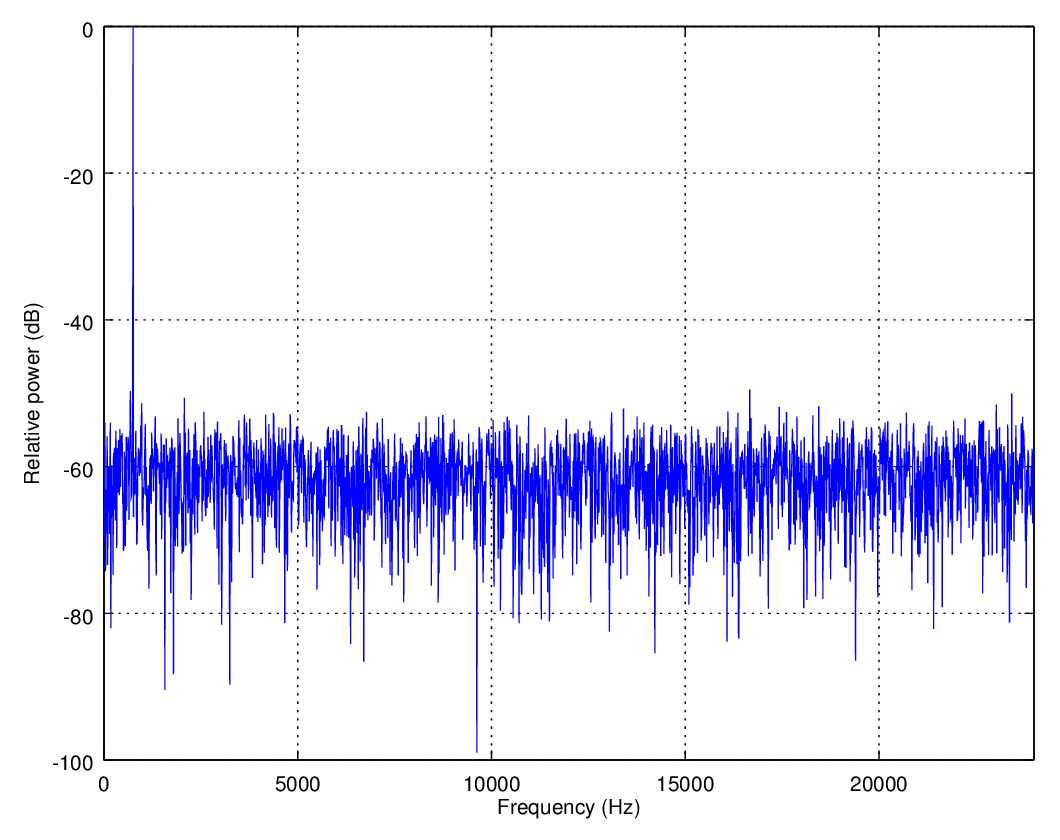
With noise-shaping, the noise floor looks like this

With 16 bits, the noise floor is down to -120 dBFS at 4 kHz, where the Fletcher-Munson curve says the ear is most sensitive (threshold of hearing at 4kHz = -5 dB SPL).
If -20 dBFS = 75 dB SPL, then -120 dBFS = -25 dB SPL. That’s 20 dB lower than the threshold of hearing.
Without noise-shaping (or less-aggressive noise-shaping), then you come closer to (but still not reaching) the threshold of audibility. But I think you’d have a hard time finding a 16-bit recording which was mastered without noise-shaping.