Hi everyone!
Have a problem. On some tracks I have digital clipping when my volume on streamer (roon end point) Fiio SR11 is 100. No matter what volume is on speakers (amplifier) cause it is digital clipping.
When i put volume in roon (sr 11 streamer) less then 88-89% the digital clipping is disappear!
Where is this problem ? How to solve it ? Cause I dont want to change volume in digital way.. Thanks!
Ps
I use Roon + Tidal
Thanks! It helps same way as digital volume control.
It reconverts signal with 64bit float.
Unfortunately, on my system any interference with the digital stream is audible â whether itâs digital volume control or (especially) using the equalizer. The dynamics drop and the timbres become noticeably poorer.
Is it impossible to overcome this without altering the digital signal? Were the specialists in the studios really that bad? It seems this happens on tracks recorded close to 0 dBâŚ
but before I started using Roon, I never had clipping issues on these same albums when playing them on a CD player!
Thereâs nothing Roon can do about clipping if you donât want it to change the bits; the streamer would have to be able to deal with it. What were you using with the CD player, and how do you know theyâre the same albums? Are they rips from the same CDs or are they coming from a service?
It seems to me that a digital problem requires a digital solution.
I have -3 dB headroom set in Roon to mitigate intersample overs, and allow headroom for filters. I turned up my preamp to compensate, and canât hear a difference. Itâs a pretty basic system.
I donât know the details of your setup, so I canât think of any other way, unless you can adjust digital volume on SR11.
Albums same, coming from Tidal with same catalog number as physical cds.
It seems this is a common and frequent issue, since Roon even created a separate thread with instructions â yet still didnât explain why it happens.
Here link: https://help.roonlabs.com/portal/en/kb/articles/dsp-engine-headroom-management
In all my long audiophile life, I have never once heard digital clipping when using a CD player.
But now I bought a streamer and Roon, and the problems began!
So what is the real reason behind this? If cd and files are digital and must be from one Master ?
What that tells me is that you havenât used the CD player with this particular streamer (probably not possible, since the SR11 doesnât seem to have coax or optical digital inputs), so the problem could be the streamer. To eliminate that suspicion, you could try using the DAC you used with the CD player with Roon, see if you still get clipping.
I donât think thatâs a guarantee youâre getting the exact same bits. To eliminate that suspicion, you could rip your CDs, import them into your Roon library, stream those instead and see if you still get clipping.
If this were a problem specific to the Fiio SR11 model, Roon would be unlikely to release a clipping-prevention feature specifically for this device only. Itâs clear that this is a general common issue.
Iâm not saying itâs a problem specific to this streamer, just that this streamer may have this particular problem. It is indeed common, but not necessarily an issue on all streamers/DACs. And, as I said, thatâs just one of the possible causes.
How is the Fiio connected to your system/amplifier?
If turning down the volume on the Fiio (via Roon) eliminates the clipping, it seems the Fiio is overdriving the input on your amp (or whatever you have the Fiioâs output connected to).
Am I missing something?
Since setting headroom eliminates the clipping issue, there is obviously no issue with the source data.
The FIIO SR11 is a digital transport. This being the case, then, unless the SR11 has a digital gain control that can exceed 0dB (which is unlikely because it would introduce exactly this issue), then surely any clipping that is happening will be occuring in the DAC to which it is connected rather than the SR11 itself.
This also fits better with my understanding of the nature of âinter-sample oversâ which is another possible cause of the issue. I have a number of DACs available to me and one in particular suffers from this issue and the 3dB headroom (or equivalent) must be employed - at least with some tracks.
Thus, the question I have surrounds the DAC. When it is stated that the same issue does not occur using the CD player, is the same DAC being used or is the analogue output of the CD player being used?
If another DAC is available, does the same clipping occur with that DAC?
Edit: If inter-sample overs is the issue, then, in Roon, you may be able to upsample the source to a higher sampling frequency (which will bring the issue into the digital domain) and then turn on the clipping indication in Roon so that you will be able to see when clipping occurs.
This exists because certain DSP settings in Roon can cause clipping, which requires a correction. And itâs explained right at the start of the article:
Digital signal processing can result in âclippingâ, or audio samples that exceed the allowed range. These samples are âclippedâ to a maximum or minimum value. In some cases, this can produce audible distortion. This is easily avoided by slightly attenuating the signal â to make âheadroomâ for sample values that may increase as a result of signal processing.
The SR11 at volume MAX/100 is bit-perfect, according to RME bit tests, at 32-bit and 44.1/48/96/192kHz.
If clippingâs indicated in Roon it must surely be due to Roonâs own DSP, perhaps because a DAC attached to the SR11 is forcing resampling to happen upstream for compatibility reasons.
If the DAC is showing clipping it could simply be due to inadequate headroom for intersample overs.
It would be good to know what DAC was being employed by the OP and to see a screen shot of the Roon signal path when streaming to that DAC via the SR11 at 100% volume.
This will tell us whether any DSP is being performed by Roon.
This isnât an explanation a reason why - itâs a just a fact statement that Roon can behave this way, and thatâs why you should enable DSP to reduce the volume.
For me, this is unacceptable. Why do I even need Roon then, if I can enjoy music from a CD player without any clipping and DSP corrections ?
DAC Flio k11 r2r operates in NOS mode.
But even in the case of upsampling no digital clipping should occur anyway.
No, this is a fundamental truth in all digital sound processing and mathematics
Instead of being upset about this, I suggest you provide the information that others already asked for, which will enable knowledgeable people to explain whatâs happening.
Every time you resample - up or down - you can get clipping, and itâs 100% dependent on the data.
Actually, with certain signal characteristics, upsampling with no other DSP operations is entirely sufficient to cause digital clipping.
Imagine single tone of amplitude A sampled at intervals of 1/4 the wavelength.
If you are lucky, you may sample it at 0, 90, 180, and 270 degrees phase resulting in values of 0, A, 0 and -A respectively.
However, you could also be sampling at 45, 135, 225 and 315 degrees of phase. In this case you will get sample values of (approximately) 0.7A, 0.7A, -0.7A and -0.7A (the correct value is the SQRT(0.5) x A)
Now imagine 0.7A is the maximum value that your encoding scheme can represent (32767 for 16 bit samples). -0.7 A is -32767 which is very nearly (but not quite) the minimum (most negative) value that your encoding scheme can represent.
Now if we resample this wave to double the sampling frequency, we effectively generate samples at 0, 45, 90, 135, 180, 225, 270, and 315 degrees phase. Thus the values that we want to represent are 0, 0.7A, A, 0.7A, 0, -0.7A, -A, -0.7A
However, since 0.7A is the maximum that can be represented and -0.7A is very nearly the minimum that can represented, we have no way to represent A or -A so clipping occurs.
With our 16 bit samples, if 0.7A results in 32768, then the A value obtained during re-sampling, would, if possible, be represented by a sample value 46341 (rounded to the nearest) which is clearly outside the range that can be represented by a signed 16 value (-32768 to 32767) and it is thus clipped.
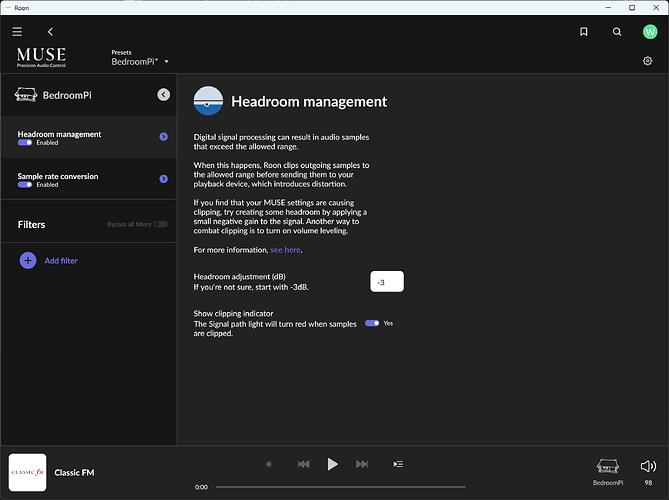
In power terms, the difference between a signal of amplitude A (that canât be represented) and one of 0.7A (which can be represented) is 20LOG10(A/0.7A) or 20LOG10(SQRT(2)) which is just slightly more than 3dB which is why a headroom value of 3dB was employed by @denydog in post 5 in this thread.
Where is the clipping indicated? From the above it sounds like it must be in the DAC, but I couldnât spot a clipping indicator on the K11 R2R.
Without a screenshot of the Roon signal path weâre still just guessing.
In Roon, enable headroom adjustment (but with the headroom set to 0dB if you donât want it to do anything) and then enable clipping indication:
As the text suggests, with this in place the signal quality dot will then turn red if clipping occurs.
If there is no clipping in Roon (signal quality is not red), then Roon is not causing the clipping and it must be happening in the DAC.
